Baby Technologies

Below is a post I wrote on Facebook when we had baby #1 and certain biological and technological situations going on. Baby #2 is here and I am glad to say we have not had any weevils, however, I have a renewed appreciation for foundational technology: dishwashers, washer-dryer and microwave! My hands would be sore without them.

===

(2017 post below)

Two technologies I was thankful for today

Or: why my wife is having a long nap and will wake to the kitchen smelling of bleach

As I was starting to mix some baby formula today, I noticed a weird bug crawling around in the kitchen. I had seen a few of these things before over the past weeks, and though I’d thought before that maybe I should call the landlord, it occurred to me to try to learn more.

These weird bugs were not ones I was familiar with. They looked like tiny horned beetles. Somehow however the word “weevil” just popped into my head as le mot juste for the creepers. I remember this word from before but couldn’t tell you anything but that they were small bugs. I suspect though that I successfully identified them sight unseen because they looked like wee evils.

Anyway the first technology to do its magic was a Google search. I looked up weevil and the first picture didn’t match, but the second one, “wheat weevil,” sure did. And lo and behold when I picked up the bag where I’d stored whole grain wheat, the little wee evils were all over the place. Apparently they lay eggs in the grain.

Thus began the industrial cleanup phase of my story. Some good non-bug-related things came out of this, e.g. I found a rotten potato before it could spoil the rest, and I threw out some rice in a container I didn’t feel was trustworthy. But it was when I was standing on a stool with my hands full of Raid that my newborn daughter, formerly asleep in her crib, decided to let out a bloodcurdling scream.

So I washed my hands and tried the usual tricks: diaper, feeding, burping, but to no avail. This brings me to the other key piece of technology, a swinging chair. Once I put her in it she decided the world was a happy place and I was able to continue my weevil murdering operation.

Lessons learned:

1. now that I make altonbrown.com/dutch-baby-pancake-recipe instead of whole grain pancakes, I shouldn’t leave piles of unused grain around the house

2. it’s never too early to set up your child’s swing

A More Intuitive Proof of Löb’s Theorem

After my previous post, I spent more time trying to better understand both of the theorems I mentioned, and want to post here a more intuitive proof of Löb’s theorem from some random planetmath URL by user dankomed, referencing this book of Podnieks. I am going to copy it out here (hopefully also being in native unicode helps legibility). I added some {brackets} where I was finding it hard to grok too many symbols in a row.

We’ll use P(·, ·) to mean proof arithmetization in a formal system F which is Peano Arithmetic or stronger, because we need Gödel’s second incompleteness theorem, which states that such systems cannot prove they are consistent (whereas the first states they can’t prove all true statements).

Löb’s theorem: If F ⊢ {∃xP(x, ň) ⇒ ϕ_n}, where x is the Gödel number of the proof of the formula with Gödel number n, and ň is the numeral of the Gödel number of the formula ϕ_n, then F ⊢ ϕ_n.

Proof: Suppose F ⊢ {∃xP(x, ň) ⇒ ϕ_n}. Let F* be the new proof system that is equal to F plus the new axiom ¬ϕ_n. By modus tollens F* ⊢ {¬ϕ_n ⇒ ¬∃xP(x, ň)}. Since F* has an axiom ¬ϕ_n by modus ponens F* ⊢ ¬∃xP(x, ň). In this case F* proves that ϕ_n is is not provable in F (and also that F is consistent). This however leads to a proof that F* is also consistent because it contains only F and ¬ϕ_n, and we already know both that F is consistent and that F does not prove ϕ_n. Thus F* proves its own consistency. According to Gödel’s second incompleteness theorem however F* cannot prove its own consistency unless it is inconsistent. Therefore F + ¬ϕ_n must always be an inconsistent theory, and we conclude that F ⊢ ϕ_n. ∎

From other pages I’ve read, I would recap it as:

• Generally, not all true statements are provable. That contradicts the first incompleteness theorem.
• Can we show that some true statements are provable? Löb’s theorem says that you can only do this when it has a proof, in which case it’s trivial. (Because if N is true, then M ⇒ N holds for any M.)
• I love this proof; it more or less shows that except for that trivial case, proving this statement about provability quickly brings you in conflict with the second incompleteness theorem (which is, as Wikipedia puts it, itself basically an arithmetization of the first incompleteness theorem). Other proofs tended to reinvent the wheel by inlining the major incompleteness theorem steps.

The corollary applying it to Henkin sentences, would I guess now go:

If S encodes “S is provable,” then S is true (because otherwise we would violate the second incompleteness theorem).

This still seems… unintuitive? If S is true, it’s provable, and you’d think we’d have an explicit proof of S itself. While the flavour is more like “we can only arrive in this situation in trivial cases.” Though for a Henkin sentence, it doesn’t feel very trivial.

Better Know a Theorem: Łoś and Löb

Over the break I finished a re-read of Gödel Escher Bach: an Eternal Golden Braid. I got the book exactly 26 years ago for Christmas from my uncle (another David Pritchard). The book is really timeless in Douglas Hofstadter’s excellent exposition of its core topics (paraphrased):

• Gödel’s incompleteness theorem: there are true statements about integers that have no formal axiomatic proof
• The Church-Turing thesis: anything that can be computed, can be computed using any computer
• The chemical basis of life: DNA encodes all your body’s functionality, including how to propagate DNA
• Art is cool: Many examples of patterns and interesting structures in the work of Escher, Bach, Magritte, Lewis Carroll and others; many cool character-based dialogues.

In re-reading it after many years, I tried to chase down any technical bits that were foreign to me, to wring it for all it’s worth. Compared to my readthrough back in the last millennium, there is a mountain of supporting information on the internet; I’m grateful since this was really helpful for my understanding of these cool theorems. Mathoverflow in particular helped me comprehend these, as I got quick answers to perplexing issues.

Both theorems are in the following context. The book spends a bunch of time looking at the expression of mathematical statements using a simplified language (TNT or “typographical number theory”), then demonstrating that proofs (built from Peano Arithmetic 1st-order axioms) can be encoded as number theory statements in TNT, finally enabling self-referential statements and the proof of Gödel’s incompleteness theorem.

Here are what I thought were the 2 most notable side nuggets:

1. Łoś’s theorem. [See “Supernatural Addition and Multiplication” within chapter XIV] The Peano axioms all hold true about the natural numbers. Are they also true about larger sets of objects? Yes! Hofstadter calls these “supernatural numbers”. Satisfying the axioms means they satisfy arithmetical properties (e.g. they form collections of sequences additively isomorphic to the integers) and also that anything which can be proven by induction holds true for them. The least weird construction is to take all infinite whole number sequences 𝐍^𝐍 and an ultrafilter (an axiom-of-choice-derived special collection of subsets of 𝐍, see a fuller definition here), with two sequences equivalent when “most” components of their sequences have the same value. Łoś’s theorem proves that this quotient satisfies all Peano axioms. (This is not the smallest model of supernatural numbers! But, the smallest model is also super weird. It’s order-isomorphic to 𝐍+(𝐐×𝐙), but it entails that neither addition nor multiplication is computable.) I highly recommend this exposition by Rising Entropy for more details, especially chapter 2 and 4 helped me a lot.
2. Löb’s Theorem. [See “Henkin Sentences and Viruses” within chapter XVI]. Gödel’s incompleteness theorem is proven by constructing a quasi-self-referential sentence S of TNT equivalent to “S has no proof in TNT”. (Incompleteness then follows as: if S has a proof, it’s true, but then it has no proof, a contradiction; so it must have no proof, and is thus true.) Löb’s Theorem asks: what’s the deal when we construct a simpler quasi-self-referential sentence S like “S does have a proof in TNT”. The deal is: they’re also always true. I find the result and proof method amazing/mystifying. (Technically Lob’s theorem is more general, this is the result of applying it to Henkin sentences.) See The Cartoon Guide here as well as Wikipedia and here and here; the boxes confused me at first as I thought my browser wasn’t rendering characters, but they’re actual math symbols. The individual steps are simple and the larger design involves lifting proofs up out of arithmetic encoding, but I lack intuition for the whole thing. [Edit: I made a new post with some additional intuition I could find from new sources.]

There are other great tidbits I learned this time around, such as how to solve the exercise “find a TNT formula for powers of 10.” There’s a beautiful proof here. The internet knows all!

PS: Props to WordPress as well for the new year

My Food Rotation

Last year as a part of moving into our place, I got a barbecue (and if you don’t count a pizza delivery, it was the genesis of the first meals we had here). The model I liked was a Napoleon and the model so happened to come with a couple of extra features:

• A side sear station. Still have no clue how this can be useful without making a giant mess
• A rotisserie rod and infrared horizontal burner to match.

Rotisserie is something I haven’t done in 40 years and so I didn’t have specific expectations, but after taking it for a spin, 2 out of 3 meals were super tasty.

• 👍 Gyros. Here I don’t mean the meatloaf-style gyros I fondly remember from the University of Waterloo plaza suite of pita restaurants, but rather the chunks-of-meat kind I fondly remember from my short time in Greece. I followed the spices here and the construction here. I couldn’t find a large whole lamb shoulder chunk, but instead deboned some lamb shoulder steaks, pounded large chunks of them to ~5mm thin, then spiced away. A couple hours later, I trimmed the crispy outer bits, let the new exposed edges get golden brown, and repeated until all gone. They were amazing fresh but also tasty for several days of leftovers.
• 👍 Ribs. I would definitely also recommend this. My notes on this are spotty… did I use an Alton Brown rib rub? did I just eyeball it with Montreal steak spice and brown sugar? who knows. I do remember it was important to accordion them on to the skewer axle. These were also super good as leftovers.
• 🆗 Rotisserie chicken. I think I have been spoiled by whatever weird laws of economics make it possible for every grocery store to sell whole pre-roasted rotisserie birds for less than a whole raw bird. I didn’t have a specific problem with the one I made, but it didn’t seem to have any appreciable oomph. Maybe I should try again with… maple syrup and mustard? Who knows

So far my next planned revolution in rotisserie cooking is to try making tacos al pastor. But for dessert: Kürtőskalács?

Ontario Voyage

At the end of the summer I was excitedly able to squeeze in a two week trip to Ontario. This wasn’t Hanna’s first rodeo, but there were several firsts for her:

• Visiting my sister’s cottage up in Nipissing District
• Going to the Ex (Canadian National Exhibition)
• Sleepover at grandma’s house

Especially because we’d been so limited in trips during covid, it was exciting to do any of this, but there were lots of great surprises even to me. For example, the picture above is a small piece of The Screaming Heads, a giant art installation not far off Highway 11. Many memorable bits of my childhood no longer exist (Weall & Cullen Miniature Village, the concrete slide ride at Blue Mountain, my great-aunt’s cottage off Lake Simcoe) but the things we found were pretty great, no aroma of tourist traps. Here’s me in a “fairy forest” of the Crystal Caves shop:

Another unexpectedly popular attraction was “porch life” at grandma’s house. Hanna made friends with a number of the neighbouring folks, enjoying a hangout with her crew most days and even making dark chocolate chip cookies to share with everyone before coming back to LA.

I deeply felt the challenge that on a trip like this, on average, you have to plan one day every day, but I think we managed pretty well. Got to see many friends and family, eat old standards (beef patties, timbits, Bibi cafe) and new tastes (pickle on a stick, Danforth’s Persian “Herby Restaurant”, doubles), and I squeezed in virtual attendance at a work summit from Google Toronto.

My sister’s cottage was amazing and a really great home base to explore an area I’d never been to before. She kept us entertained with a great BBQ, hiking, and Kerplunk. My brother’s vintage 1980s Ninja Turtles were a hit back in Scarborough and we also went to Hanna’s first Chuck E Cheese, so I think I have to say we did well on the nostalgia front.

Slight disaster on the last day (missed flight by 4 minutes) turned into mild bureaucratic elation as we managed to get a walk-in appointment to renew Hanna’s Nexus card and squeeze in one last round of mini-golf near YYZ. See you next time Canada!

Edmonton Sportsball Team

References:

• https://www.reddit.com/r/sbubby/comments/spcsb5/oilers_formula/
• https://www.kickstarter.com/projects/1004050824/the-euler-oiler-tee-shirt/posts/1920830
• https://divisbyzero.com/2010/11/11/the-edmonton-eulers/

10 California Breweries

This holiday season, I decided it would be interesting to make notes about the different beers I would try over the next year. Maybe it was the fact that Trump was still president, but it certainly seemed like a drinking experiment could lead to some new discoveries.

So far, I’ve kept the experiment running for a month. As such, I wanted to dive into a slice of the data. Below are the beers I’ve had from California in one month. Here, I’ve sorted them from north to south.

Brewery	# Beers	Quality	Interesting?
Lost Coast Brewery	1	6 (Okay)	7 (Good)
Sierra Nevada Brewing Co	3	6-8 (Ok-Very Good)	6-7
Anderson Valley Brewing Co	1	7	7
Russian River Brewing Company	1	8	7
Josephsbrau Brewing Co. (Gordon Biersch via Trader Joe’s)	1	6	9 (Excellent)
Full Circle Brewing Co.	1	5 (Borderline)	8
Santa Monica Brew Works	3	6-7	5-7
Los Angeles Ale Works	1	7	6.5
Modern Times	2	8	7-8
Coronado Brewing Co	1	8	8

California beer data

Conclusions:

• Most interesting California beer: Ginger Beard Spiced Stout from Josephsbrau/Trader Joe’s. My notes: Gingerbread on the nose. Not super drinkable but remarkable and palatable.
• Where I should retire to become a beer sommelier: San Diego (home of Modern Times, Coronado)
• Best (and only) brewery within stumbling distance: Santa Monica Brew Works

Computer Science Circles: 10 years + 2 million problems

The longest-running project I’ve ever been involved with just turned 10! Computer Science Circles (https://cscircles.cemc.uwaterloo.ca) is a website that teaches introductory programming via Python. It has automatically-graded programming exercises, and in addition, students and teachers can register together, using the site as a place to ask/answer questions and track progress.

The ruminations and brainstorming for the website began in 2009. The name is similar to Math Circles, though Troy also justified it thusly:

I imagined the circles perhaps overlapping in some Venn-like way: doing this module in language X leads to a similar language in language Y. Or maybe they are even touching at various points: go around the Python Circle, and it connects at other points.

Whatever curvature we obtained, the project worked pretty well. At the time of writing, 1,993,555 problems have been solved on the site, with the most popular problem solved by 58,298 registered accounts. (And 1601 accounts have solved the hardest problem.)

We finally decided to ditch our original webserver this year. To that end, I thought some comparisons would be apt:

	2010-2011	2019
What happened:	Site launched! (First users Sept 2011)	New server!
The WordPress:	2.9.2 “Carmen McRae” (Installed May 20, 2010)	5.3 “Rahsaan Roland Kirk”
The hot newness:	Python 3	WordPress upgrades with a button click
The crufty oldness:	Python 2	Role Scoper, a plugin last updated 3 years ago that I had to delete
OS	CentOS 5.x (too obsolete for recent PHP)	Ubuntu 18.04
Localizations	English, French, …	…, German, Dutch, Chinese, Lithuanian

Troy, Sandy and I still answer questions from students on the site. It definitely has been helpful to split the load three ways, but the number of questions was never aggressively overwhelming. There are multiple places online where answers are posted and I wonder to what extent that contributed 🙂

Probably the hardest single maintenance issue over time was when we wanted to add HTTPS to the old server. The awesome letsencrypt.org project gave us a way to do it—sort of—hacking around the incompatibly old PHP version to somehow run the acme certbot. Anyway. The overall construction and maintenance of everything added up to about 2k commits in total on github.

In addition to a paper and a couple of posters on the site itself, the most interesting outcomes to me have been:

• visiting a jail in Penetanguishene where they cloned the open-source version to teach this without internet access
• a 2015 paper on frequency distributions of programming errors, using the CS Circles submissions corpus
• a 2016 paper with educators at a Serbian university on extensions they added to their fork of the site

What do I hope to accomplish in the next 10 years of Computer Science Circles?

• I’ve been using git subrepositories for ten years, and I still have no idea how they work and how to properly maintain them… that seems like worth learning since I’ve broken things more than once as a result.
• New content: maybe idiomatic Python data structures such as dictionaries?
• More localizations. We’ve had multiple false starts on different languages and it would be nice to get another big one out the door (e.g. Spanish).

Last but not least I owe a debt to all the free software on which the site was built, including Linux, Python, WordPress, CodeMirror, Polylang, and FlexiGrid; Mooshak, which we built our safeexec from; and Philip Guo and Peter Wentworth who built the original visualizer and its Python 3 port.

A Tale of Two Boxes

Back in New Jersey, we subscribed to the Great Road Farm CSA service for a year. Since we were basically in the middle of a bunch of farmland, it worked out great and I got some keeper recipes out of it like this Kale and White Bean soup. Moving forward a couple of years and on the one hand we currently live in the concrete jungle of Santa Monica, but on the other hand it’s California which is well-known for its produce.

I eventually got my vegetable game together and signed up for two CSAs here:

1. Out Of The Box Collective, which came to Google Earth Day a couple of years ago
2. Good Life Organics, which I found on Yelp

Though we cancelled these during our trip to Canada this year, when we came back I thought to take a more careful look at these. I remember some high and low points from the past:

• Good Life Organics gave me an awesome fresh herb bundle just before thanksgiving last year: sage, bay, rosemary and thyme. That ended up used in the turkey, the stuffing, the soup and in other goodies, which was great since buying them individually is usually an expensive waste.
• On the other hand, Good Life Organics also gave me a huge daikon radish back in February. Like, a one-pounder. Wasn’t very useful; one person can only eat so many bitter daikon pickles.

I’d signed up for the smallest box each service has to offer. With Out Of The Box this is $49, plus a $5 delivery fee, and with Good Life, it is $27, and we pick it up at a nearby address. In order to decide which one to stick with, I took some photos to document our most recent pair of boxes.

Out Of The Box

For my delivery this month, I got:

• a few things that I grilled: 1 cantaloupe, 3 shishito peppers, 2 zucchini
• ~2 lbs tomatoes, some of which I grilled, and the rest of which became persian omelette
• the world’s saddest head of butter lettuce and mini-herb bundles
• a package of watercress and a box of grapes, mislabeled as seedless
• some staples: avocado, cucumber, garlic, lime, onion

Overall, they’ve had better boxes. When I tried to estimate the total cost compared to buying individually, it was a pretty high price.

Good Life Organics

This box contained:

• 2 each of pluots, plums and nectarines
• a canary melon and a box of seedless grapes
• roma tomatoes and onion that became part of a pasta sauce
• a whole box of shishito peppers which were awesome sauteed
• an avocado which Hanna ate whole over the course of several meals
• a bunch of rainbow carrots

Drumroll please… we ended up cancelling our Out Of The Box subscription and decided to go with just Good Life Organics. I’m still not convinced it’s much cheaper than buying à la carte but at least it gets us eating more fruits + veggies and gives us some variety. I’ll have to try harder to find a good application for the next daikon they send me.

Family Tree Visualizer

I remember once, long ago in high school, there was some project where I had to look up and draw my family tree. Being the not-so-organized guy that I am, I lost that specific project many years ago. But since then, I also had a whole bunch of changes to the tree: I visited Iran and met all my spouse’s cousins, and we welcomed a new baby. The arrival of the little one gave me some motivation to take the tree I scribbled down about my in-laws and combine it, along with my parents and siblings’ info.

Who doesn’t love recursion? I thought it would therefore be a fun exercise to write a program to draw the tree. On top of which, I’m a lot less likely to lose the data again if I save it somewhere online. So in January I started making some super basic prototypes in Python. After some iterations, including one that I printed out and was about 8 feet wide, I uploaded the current web JavaScript version to GitHub this month.

Here’s what it looks like — you can access the interactive web interface at https://daveagp.github.io/family-tree:

This, of course, is the Simpsons. I figured it is maybe not a great idea to publish all the information about my family to a public place and that’s why I created a mock tree for the GitHub repository. On the other hand, in the course of looking up information on past relatives, I ran across geni.com which has exactly that: family tree information that various folks have posted publicly online (and in my case, I did actually find information on relatives some generations back). Long story short, the visualizer with own real family tree is online but behind a password, if you’re interested to see just email me to ask how to see it.

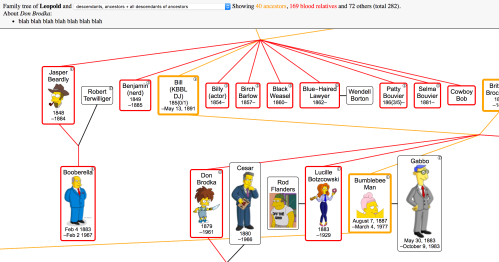
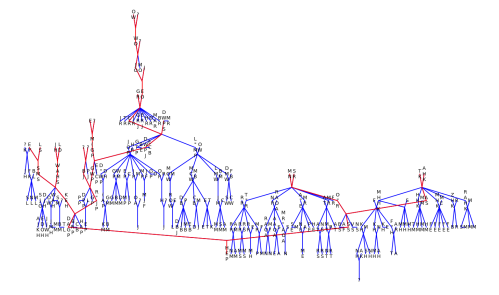In January, I started with a very basic prototype which generated something like this:Its initial purpose was to help me figure out the input biographical record format and get an idea on what would be the simplest working layout algorithm. Fast forward a while to the past couple days, when I took the “finished” JavaScript version and tried to figure out what the heck my own code is doing. Recursion is complicated! I’m now pretty happy with the state of the code (https://github.com/daveagp/family-tree), having separated the styling, visibility, and geometric layout logic. The basic tree layout algorithm is this:

• The initial recursive call is to lay out the tree for some “root” user.
• There are “nodes” both for every user, and for every union (marriage/child-bearing couple).
• To lay out the tree for a node,
  • first lay out trees for every node one step further from the root.
  • then combine these trees, fitting them side by side and adding the node in question.

The current version creates very long horizontal edges leading to ancestors of the root (which you can see also in the prototype), though I think these are difficult to avoid if you also want to respect the left-to-right layout of children of each family as going from first-to-last born. It would be interesting to see what arises from other layout algorithms.